Logistic Regression to Create Classification Models
Case Study: Income group classification(WHO data) using Logistic Regression
Context:
- DeltaSquare is an NGO that works with the Government on matters of social policy to bring about a change in the lives of underprivileged sections of society. They are tasked with coming up with a policy framework by looking at the data government got from WHO. You as a data scientist at DeltaSquare are tasked with solving this problem and sharing a proposal for the government.
Problem:
The data-set aims to answer the following key questions:
- What are the different factors that influence the income of an individual?
- Is there a good predictive model for income that exists? What does the performance assessment look like for such a model?
Attribute Information:
- The data contains characteristics of the people
- age: continuous – age of a Person
- workclass: Where do a person works – categorical -Private, Self-emp-not-inc, Self-emp-inc, Federal-gov, Local-gov, State-gov, Without-pay, Never-worked.
- fnlwgt: This weight is assigned by the Current Population Survey (CPS). People with similar demographic characteristics should have similar weights since it is a feature aimed to allocate similar weights to people with similar demographic characteristics – continuous
- education: Degree the person has – Bachelors, Some-college, 11th, HS-grad, Prof-school, Assoc-acdm, Assoc-voc, 9th, 7th-8th, 12th, Masters, 1st-4th, 10th, Doctorate, 5th-6th, Preschool.
- education-num: no. of years a person studied – continuous.
- marital-status: Married-civ-spouse, Divorced, Never-married, Separated, Widowed, Married-spouse-absent, Married-AF-spouse.
- occupation: Tech-support, Craft-repair, Other-service, Sales, Exec-managerial, Prof-specialty, Handlers-cleaners, Machine-op-inspct, Adm-clerical, Farming-fishing, Transport-moving, Priv-house-serv, Protective-serv, Armed-Forces.
- relationship: Wife, Own-child, Husband, Not-in-family, Other-relative, Unmarried.
- race: White, Asian-Pac-Islander, Amer-Indian-Eskimo, Other, Black.
- sex: Female, Male.
- capital-gain: Investment gain of the person other than salary – continuous
- capital-loss: Loss from investments – continuous
- hours-per-week: No. of hours a person works – continuous.
- native-country: United-States, Cambodia, England, Puerto-Rico, Canada, Germany, Outlying-US(Guam-USVI-etc), India, Japan, Greece, South, China, Cuba, Iran, Honduras, Philippines, Italy, Poland, Jamaica, Vietnam, Mexico, Portugal, Ireland, France, Dominican-Republic, Laos, Ecuador, Taiwan, Haiti, Columbia, Hungary, Guatemala, Nicaragua, Scotland, Thailand, Yugoslavia, El-Salvador, Trinadad&Tobago, Peru, Hong, Holand-Netherlands.
- salary: >50K, <=50K (dependent variable, the salary is in Dollars per year)
Learning Outcomes:
- Exploratory Data Analysis
- Preparing the data to train a model
- Training and understanding of data using a logistic regression model
- Model evaluation
Steps and Tasks:
- Import Libraries and Load Dataset
- Overview of data
- Data Visualization
- Data preparation
- Choose Model, Train, and Evaluate
- Conclusion
DataSet:
Solutions Notebook:
Loading Libraries
In [ ]:
# this will help in making the Python code more structured automatically (good coding practice)
%load_ext nb_black
import warnings
warnings.filterwarnings("ignore")
# Libraries to help with reading and manipulating data
import pandas as pd
import numpy as np
# Library to split data
from sklearn.model_selection import train_test_split
# libaries to help with data visualization
import matplotlib.pyplot as plt
import seaborn as sns
# Removes the limit for the number of displayed columns
pd.set_option("display.max_columns", None)
# Sets the limit for the number of displayed rows
pd.set_option("display.max_rows", 200)
# To build model for prediction
from sklearn.linear_model import LogisticRegression
s
# To get diferent metric scores
from sklearn.metrics import (
f1_score,
accuracy_score,
recall_score,
precision_score,
confusion_matrix,
roc_auc_score,
plot_confusion_matrix,
precision_recall_curve,
roc_curve,
)
Load data
In [ ]:
who = pd.read_csv("who_data.csv")
In [ ]:
# copying data to another variable to avoid any changes to original data data = who.copy()
View the first and last 5 rows of the dataset.
In [ ]:
data.head()
Out[ ]:
| age | workclass | fnlwgt | education | education_no_of_years | marital_status | occupation | relationship | race | sex | capital_gain | capital_loss | working_hours_per_week | native_country | salary | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 39 | State-gov | 77516 | Bachelors | 13 | Never-married | Adm-clerical | Not-in-family | White | Male | 2174 | 0 | 40 | United-States | <=50K |
| 1 | 50 | Self-emp-not-inc | 83311 | Bachelors | 13 | Married-civ-spouse | Exec-managerial | Husband | White | Male | 0 | 0 | 13 | United-States | <=50K |
| 2 | 38 | Private | 215646 | HS-grad | 9 | Divorced | Handlers-cleaners | Not-in-family | White | Male | 0 | 0 | 40 | United-States | <=50K |
| 3 | 53 | Private | 234721 | 11th | 7 | Married-civ-spouse | Handlers-cleaners | Husband | Black | Male | 0 | 0 | 40 | United-States | <=50K |
| 4 | 28 | Private | 338409 | Bachelors | 13 | Married-civ-spouse | Prof-specialty | Wife | Black | Female | 0 | 0 | 40 | Cuba | <=50K |
Understand the shape of the dataset.
In [ ]:
data.shape
Out[ ]:
(32561, 15)
- The dataset has 32561 rows and 14 columns
Let’s create a list of numerical and categorical columns
In [ ]:
numeric_cols = data.select_dtypes(include=[np.number]).columns
cat_cols = data.describe(include=["object"]).columns
print("Categorical Columns: ", cat_cols)
print("Numeric Columns: ", numeric_cols)
Categorical Columns: Index(['workclass', 'education', 'marital_status', 'occupation',
'relationship', 'race', 'sex', 'native_country', 'salary'],
dtype='object')
Numeric Columns: Index(['age', 'fnlwgt', 'education_no_of_years', 'capital_gain',
'capital_loss', 'working_hours_per_week'],
dtype='object')
Summary of the numerical data
In [ ]:
data.describe().T
Out[ ]:
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| age | 32561.0 | 38.581647 | 13.640433 | 17.0 | 28.0 | 37.0 | 48.0 | 90.0 |
| fnlwgt | 32561.0 | 189778.366512 | 105549.977697 | 12285.0 | 117827.0 | 178356.0 | 237051.0 | 1484705.0 |
| education_no_of_years | 32561.0 | 10.080679 | 2.572720 | 1.0 | 9.0 | 10.0 | 12.0 | 16.0 |
| capital_gain | 32561.0 | 1077.648844 | 7385.292085 | 0.0 | 0.0 | 0.0 | 0.0 | 99999.0 |
| capital_loss | 32561.0 | 87.303830 | 402.960219 | 0.0 | 0.0 | 0.0 | 0.0 | 4356.0 |
| working_hours_per_week | 32561.0 | 40.437456 | 12.347429 | 1.0 | 40.0 | 40.0 | 45.0 | 99.0 |
age: Average age of people in the dataset is 38 years, age has a wide range from 17 to 90 years.education_no_of_years: The average education in years is 10 years. There’s a large difference between the minimum value and 25th percentile which indicates that there might be outliers present in this variable.capital_gain: There’s a huge difference in the 75th percentile and maximum value of capital_gain indicating the presence of outliers. Also, 75% of the observations are 0.capital_loss: Same as capital gain there’s a huge difference in the 75th percentile and maximum value indicating the presence of outliers. Also, 75% of the observations are 0.working_hours_per_week: On average people work for 40 hours a week. A vast difference in minimum value and 25th percentile, as well as 75th percentile and the maximum value, indicates that there might be outliers present in the variable.
Checking different levels in categorical data
In [ ]:
# Checking value counts of categorical variables
for i in cat_cols:
print("Unique values in", i, "are :")
print(data[i].value_counts())
print("*" * 50)
print(data[i].value_counts(1))
print("*" * 50)
Unique values in workclass are : Private 22696 Self-emp-not-inc 2541 Local-gov 2093 ? 1836 State-gov 1298 Self-emp-inc 1116 Federal-gov 960 Without-pay 14 Never-worked 7 Name: workclass, dtype: int64 ************************************************** Private 0.697030 Self-emp-not-inc 0.078038 Local-gov 0.064279 ? 0.056386 State-gov 0.039864 Self-emp-inc 0.034274 Federal-gov 0.029483 Without-pay 0.000430 Never-worked 0.000215 Name: workclass, dtype: float64 ************************************************** Unique values in education are : HS-grad 10501 Some-college 7291 Bachelors 5355 Masters 1723 Assoc-voc 1382 11th 1175 Assoc-acdm 1067 10th 933 7th-8th 646 Prof-school 576 9th 514 12th 433 Doctorate 413 5th-6th 333 1st-4th 168 Preschool 51 Name: education, dtype: int64 ************************************************** HS-grad 0.322502 Some-college 0.223918 Bachelors 0.164461 Masters 0.052916 Assoc-voc 0.042443 11th 0.036086 Assoc-acdm 0.032769 10th 0.028654 7th-8th 0.019840 Prof-school 0.017690 9th 0.015786 12th 0.013298 Doctorate 0.012684 5th-6th 0.010227 1st-4th 0.005160 Preschool 0.001566 Name: education, dtype: float64 ************************************************** Unique values in marital_status are : Married-civ-spouse 14976 Never-married 10683 Divorced 4443 Separated 1025 Widowed 993 Married-spouse-absent 418 Married-AF-spouse 23 Name: marital_status, dtype: int64 ************************************************** Married-civ-spouse 0.459937 Never-married 0.328092 Divorced 0.136452 Separated 0.031479 Widowed 0.030497 Married-spouse-absent 0.012837 Married-AF-spouse 0.000706 Name: marital_status, dtype: float64 ************************************************** Unique values in occupation are : Prof-specialty 4140 Craft-repair 4099 Exec-managerial 4066 Adm-clerical 3770 Sales 3650 Other-service 3295 Machine-op-inspct 2002 ? 1843 Transport-moving 1597 Handlers-cleaners 1370 Farming-fishing 994 Tech-support 928 Protective-serv 649 Priv-house-serv 149 Armed-Forces 9 Name: occupation, dtype: int64 ************************************************** Prof-specialty 0.127146 Craft-repair 0.125887 Exec-managerial 0.124873 Adm-clerical 0.115783 Sales 0.112097 Other-service 0.101195 Machine-op-inspct 0.061485 ? 0.056601 Transport-moving 0.049046 Handlers-cleaners 0.042075 Farming-fishing 0.030527 Tech-support 0.028500 Protective-serv 0.019932 Priv-house-serv 0.004576 Armed-Forces 0.000276 Name: occupation, dtype: float64 ************************************************** Unique values in relationship are : Husband 13193 Not-in-family 8305 Own-child 5068 Unmarried 3446 Wife 1568 Other-relative 981 Name: relationship, dtype: int64 ************************************************** Husband 0.405178 Not-in-family 0.255060 Own-child 0.155646 Unmarried 0.105832 Wife 0.048156 Other-relative 0.030128 Name: relationship, dtype: float64 ************************************************** Unique values in race are : White 27816 Black 3124 Asian-Pac-Islander 1039 Amer-Indian-Eskimo 311 Other 271 Name: race, dtype: int64 ************************************************** White 0.854274 Black 0.095943 Asian-Pac-Islander 0.031909 Amer-Indian-Eskimo 0.009551 Other 0.008323 Name: race, dtype: float64 ************************************************** Unique values in sex are : Male 21790 Female 10771 Name: sex, dtype: int64 ************************************************** Male 0.669205 Female 0.330795 Name: sex, dtype: float64 ************************************************** Unique values in native_country are : United-States 29170 Mexico 643 ? 583 Philippines 198 Germany 137 Canada 121 Puerto-Rico 114 El-Salvador 106 India 100 Cuba 95 England 90 Jamaica 81 South 80 China 75 Italy 73 Dominican-Republic 70 Vietnam 67 Guatemala 64 Japan 62 Poland 60 Columbia 59 Taiwan 51 Haiti 44 Iran 43 Portugal 37 Nicaragua 34 Peru 31 France 29 Greece 29 Ecuador 28 Ireland 24 Hong 20 Cambodia 19 Trinadad&Tobago 19 Laos 18 Thailand 18 Yugoslavia 16 Outlying-US(Guam-USVI-etc) 14 Honduras 13 Hungary 13 Scotland 12 Holand-Netherlands 1 Name: native_country, dtype: int64 ************************************************** United-States 0.895857 Mexico 0.019748 ? 0.017905 Philippines 0.006081 Germany 0.004207 Canada 0.003716 Puerto-Rico 0.003501 El-Salvador 0.003255 India 0.003071 Cuba 0.002918 England 0.002764 Jamaica 0.002488 South 0.002457 China 0.002303 Italy 0.002242 Dominican-Republic 0.002150 Vietnam 0.002058 Guatemala 0.001966 Japan 0.001904 Poland 0.001843 Columbia 0.001812 Taiwan 0.001566 Haiti 0.001351 Iran 0.001321 Portugal 0.001136 Nicaragua 0.001044 Peru 0.000952 France 0.000891 Greece 0.000891 Ecuador 0.000860 Ireland 0.000737 Hong 0.000614 Cambodia 0.000584 Trinadad&Tobago 0.000584 Laos 0.000553 Thailand 0.000553 Yugoslavia 0.000491 Outlying-US(Guam-USVI-etc) 0.000430 Honduras 0.000399 Hungary 0.000399 Scotland 0.000369 Holand-Netherlands 0.000031 Name: native_country, dtype: float64 ************************************************** Unique values in salary are : <=50K 24720 >50K 7841 Name: salary, dtype: int64 ************************************************** <=50K 0.75919 >50K 0.24081 Name: salary, dtype: float64 **************************************************
- There are some values represented by a ‘?’ in workclass, occupation, and native country columns which we should investigate further.
- There are many distinct values in native_country that can be reduced to their respective continents.
- The distinct levels of marital_status can also be reduced.
Data Cleaning
We can assume that wherever there is a ? the data is unknown or missing. Let us see if there is a pattern in the missingness.
workclass
In [ ]:
data[data["workclass"] == " ?"].sample(5)
Out[ ]:
| age | workclass | fnlwgt | education | education_no_of_years | marital_status | occupation | relationship | race | sex | capital_gain | capital_loss | working_hours_per_week | native_country | salary | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9577 | 35 | ? | 119006 | HS-grad | 9 | Widowed | ? | Own-child | White | Female | 0 | 0 | 38 | United-States | <=50K |
| 2356 | 22 | ? | 196943 | Some-college | 10 | Separated | ? | Own-child | White | Male | 0 | 0 | 25 | United-States | <=50K |
| 29614 | 25 | ? | 219897 | Masters | 14 | Never-married | ? | Not-in-family | White | Female | 0 | 0 | 35 | Canada | <=50K |
| 13646 | 62 | ? | 129246 | HS-grad | 9 | Married-civ-spouse | ? | Husband | White | Male | 0 | 0 | 40 | United-States | <=50K |
| 16130 | 20 | ? | 369678 | HS-grad | 9 | Never-married | ? | Not-in-family | Other | Male | 0 | 0 | 43 | United-States | <=50K |
- From the sample it looks like wherever workclass is missing occupation is also missing.
- It looks like for ? observations in workclass the native country is the United States.
- Let’s see if the above observations hold.
In [ ]:
data[data["workclass"] == " ?"]["occupation"].value_counts()
Out[ ]:
? 1836 Name: occupation, dtype: int64
- It is indeed true that wherever workclass has ? the occupation is also ?
- This indicates there is a strong pattern in the missingness of workclass and occupation. This is intuitive as well because both the columns are capturing similar information.
In [ ]:
data[data["workclass"] == " ?"]["native_country"].value_counts()
Out[ ]:
United-States 1659 Mexico 33 ? 27 Canada 14 Philippines 10 South 9 Germany 9 Taiwan 9 China 7 El-Salvador 6 Italy 5 Puerto-Rico 5 Poland 4 England 4 Portugal 3 Columbia 3 Vietnam 3 Dominican-Republic 3 Japan 3 Cuba 3 Haiti 2 France 2 Ecuador 1 Peru 1 Cambodia 1 Thailand 1 Honduras 1 Laos 1 Hong 1 Guatemala 1 Trinadad&Tobago 1 Iran 1 Nicaragua 1 Jamaica 1 Scotland 1 Name: native_country, dtype: int64
- The above observations don’t hold for native_country as there many other countries where the observations are ?.
occupation
In [ ]:
data[data["occupation"] == " ?"].sample(5)
Out[ ]:
| age | workclass | fnlwgt | education | education_no_of_years | marital_status | occupation | relationship | race | sex | capital_gain | capital_loss | working_hours_per_week | native_country | salary | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 23936 | 19 | ? | 217194 | 10th | 6 | Never-married | ? | Own-child | White | Male | 0 | 0 | 30 | United-States | <=50K |
| 4812 | 69 | ? | 164102 | HS-grad | 9 | Divorced | ? | Not-in-family | White | Female | 0 | 0 | 40 | United-States | >50K |
| 30208 | 17 | ? | 34019 | 10th | 6 | Never-married | ? | Own-child | White | Male | 0 | 0 | 20 | United-States | <=50K |
| 8805 | 20 | ? | 216563 | 11th | 7 | Never-married | ? | Other-relative | White | Male | 0 | 0 | 40 | United-States | <=50K |
| 30061 | 33 | ? | 393376 | 11th | 7 | Never-married | ? | Not-in-family | White | Female | 0 | 0 | 40 | United-States | <=50K |
In [ ]:
data[data["occupation"] == " ?"]["workclass"].value_counts()
Out[ ]:
? 1836 Never-worked 7 Name: workclass, dtype: int64
- We observe the same pattern here, where occupation is ? most of the values in workclass are ?.
In [ ]:
data[data["occupation"] == " ?"]["native_country"].value_counts()
Out[ ]:
United-States 1666 Mexico 33 ? 27 Canada 14 Philippines 10 South 9 Germany 9 Taiwan 9 China 7 El-Salvador 6 Italy 5 Puerto-Rico 5 Poland 4 England 4 Portugal 3 Columbia 3 Vietnam 3 Dominican-Republic 3 Japan 3 Cuba 3 Haiti 2 France 2 Ecuador 1 Peru 1 Cambodia 1 Thailand 1 Honduras 1 Laos 1 Hong 1 Guatemala 1 Trinadad&Tobago 1 Iran 1 Nicaragua 1 Jamaica 1 Scotland 1 Name: native_country, dtype: int64
- The native_country column has other countries where the observations are ? corresponding to ?s in occupation.
native_country
In [ ]:
data[data["native_country"] == " ?"].sample(5)
Out[ ]:
| age | workclass | fnlwgt | education | education_no_of_years | marital_status | occupation | relationship | race | sex | capital_gain | capital_loss | working_hours_per_week | native_country | salary | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30230 | 20 | Private | 178469 | HS-grad | 9 | Never-married | Other-service | Own-child | Asian-Pac-Islander | Female | 0 | 0 | 15 | ? | <=50K |
| 16381 | 20 | Private | 219835 | Some-college | 10 | Never-married | Sales | Own-child | White | Male | 0 | 0 | 30 | ? | <=50K |
| 28220 | 70 | Private | 237065 | 5th-6th | 3 | Widowed | Other-service | Other-relative | White | Female | 2346 | 0 | 40 | ? | <=50K |
| 15678 | 42 | Self-emp-not-inc | 183765 | Bachelors | 13 | Never-married | Prof-specialty | Not-in-family | White | Male | 0 | 0 | 50 | ? | <=50K |
| 8477 | 24 | Private | 178255 | Some-college | 10 | Married-civ-spouse | Priv-house-serv | Wife | White | Female | 0 | 0 | 40 | ? | <=50K |
In [ ]:
data[data["native_country"] == " ?"]["occupation"].value_counts()
Out[ ]:
Prof-specialty 102 Other-service 83 Exec-managerial 74 Craft-repair 69 Sales 66 Adm-clerical 49 Machine-op-inspct 36 ? 27 Transport-moving 25 Handlers-cleaners 20 Tech-support 16 Priv-house-serv 6 Farming-fishing 5 Protective-serv 5 Name: occupation, dtype: int64
In [ ]:
data[data["native_country"] == " ?"]["workclass"].value_counts()
Out[ ]:
Private 410 Self-emp-not-inc 42 Self-emp-inc 42 ? 27 Local-gov 26 State-gov 19 Federal-gov 17 Name: workclass, dtype: int64
- There is no clear pattern here.
Observations:
- We observe that all the observations where workclass = ? the values in the occupation are ?
- The strong pattern between workclass and occupation makes sense as both of these variables capture similar information.
- There is no strong correlation of ? observations in occupation and workclass with native_country.
- For now we will replace these ?’s with the ‘unknown’ category.
Replacing ? with ‘Unknown’
In [ ]:
data.workclass = data.workclass.apply(lambda x: "Unknown" if x == " ?" else x) data.native_country = data.native_country.apply(lambda x: "Unknown" if x == " ?" else x) data.occupation = data.occupation.apply(lambda x: "Unknown" if x == " ?" else x)
Mapping countries to continents to reduce the number of unique values.
In [ ]:
data.native_country.nunique()
Out[ ]:
42
- There are 42 distinct countries in the data set, we can reduce them to their respective continents as this will help us reduce the dimension of data.
In [ ]:
data.native_country = data.native_country.str.replace(
" ", ""
) # remove empty spaces from strings
In [ ]:
north_america = [
"Canada",
"Cuba",
"Dominican-Republic",
"El-Salvador",
"Guatemala",
"Haiti",
"Honduras",
"Jamaica",
"Mexico",
"Nicaragua",
"Outlying-US(Guam-USVI-etc)",
"Puerto-Rico",
"Trinadad&Tobago",
"United-States",
]
asia = [
"Cambodia",
"China",
"Hong",
"India",
"Iran",
"Japan",
"Laos",
"Philippines",
"Taiwan",
"Thailand",
"Vietnam",
]
south_america = ["Columbia", "Ecuador", "Peru"]
europe = [
"England",
"France",
"Germany",
"Greece",
"Holand-Netherlands",
"Hungary",
"Ireland",
"Italy",
"Poland",
"Portugal",
"Scotland",
"Yugoslavia",
]
other = ["South", "Unknown", "?"]
In [ ]:
def region_combining(x):
if x in north_america:
return "north_america"
elif x in asia:
return "asia"
elif x in south_america:
return "south_america"
elif x in europe:
return "europe"
elif x in other:
return "other"
else:
return x
In [ ]:
data["native_country"] = data["native_country"].apply(region_combining)
In [ ]:
print("Distinct values in Native Country column:", data.native_country.nunique())
Distinct values in Native Country column: 5
Reducing the number of distinct values in marital_status
In [ ]:
data.marital_status.unique()
Out[ ]:
array([' Never-married', ' Married-civ-spouse', ' Divorced',
' Married-spouse-absent', ' Separated', ' Married-AF-spouse',
' Widowed'], dtype=object)
We can reduce these values into the following groups:
- Married
- Not-Married
- Never-Married
In [ ]:
data.marital_status = data.marital_status.str.replace(
" ", ""
) # remove empty spaces from strings
married = ["Married-civ-spouse", "Married-AF-spouse"]
not_married = ["Divorced", "Separated", "Widowed", "Married-spouse-absent"]
def reduce_marital_status(x):
if x in married:
return "married"
elif x in not_married:
return "not_married"
else:
return x
In [ ]:
data.marital_status = data.marital_status.apply(reduce_marital_status)
In [ ]:
data.marital_status.unique()
Out[ ]:
array(['Never-married', 'married', 'not_married'], dtype=object)
- Values have been clubbed into three categories.
In [ ]:
df_clean = data.copy()
Let’s explore the data in depth
Note: The EDA section of the notebook has been covered multiple times in the previous case studies. For this discussion, EDA section can be skipped and we can refer to the EDA summary below. For the detailed EDA, Appendix Section can be referred.
The below three functions need to be defined to carry out the Exploratory Data Analysis.
In [ ]:
# function to create labeled barplots
def labeled_barplot(data, feature, perc=False, n=None):
"""
Barplot with percentage at the top
data: dataframe
feature: dataframe column
perc: whether to display percentages instead of count (default is False)
n: displays the top n category levels (default is None, i.e., display all levels)
"""
total = len(data[feature]) # length of the column
count = data[feature].nunique()
if n is None:
plt.figure(figsize=(count + 1, 5))
else:
plt.figure(figsize=(n + 1, 5))
plt.xticks(rotation=90, fontsize=15)
ax = sns.countplot(
data=data,
x=feature,
palette="Paired",
order=data[feature].value_counts().index[:n].sort_values(),
)
for p in ax.patches:
if perc == True:
label = "{:.1f}%".format(
100 * p.get_height() / total
) # percentage of each class of the category
else:
label = p.get_height() # count of each level of the category
x = p.get_x() + p.get_width() / 2 # width of the plot
y = p.get_height() # height of the plot
ax.annotate(
label,
(x, y),
ha="center",
va="center",
size=12,
xytext=(0, 5),
textcoords="offset points",
) # annotate the percentage
plt.show() # show the plot
In [ ]:
def stacked_barplot(data, predictor, target):
"""
Print the category counts and plot a stacked bar chart
data: dataframe
predictor: independent variable
target: target variable
"""
count = data[predictor].nunique()
sorter = data[target].value_counts().index[-1]
tab1 = pd.crosstab(data[predictor], data[target], margins=True).sort_values(
by=sorter, ascending=False
)
print(tab1)
print("-" * 120)
tab = pd.crosstab(data[predictor], data[target], normalize="index").sort_values(
by=sorter, ascending=False
)
tab.plot(kind="bar", stacked=True, figsize=(count + 5, 5))
plt.legend(
loc="lower left", frameon=False,
)
plt.legend(loc="upper left", bbox_to_anchor=(1, 1))
plt.show()
In [ ]:
### function to plot distributions wrt target
def distribution_plot_wrt_target(data, predictor, target):
fig, axs = plt.subplots(2, 2, figsize=(12, 10))
target_uniq = data[target].unique()
axs[0, 0].set_title("Distribution of target for target=" + str(target_uniq[0]))
sns.histplot(
data=data[data[target] == target_uniq[0]],
x=predictor,
kde=True,
ax=axs[0, 0],
color="teal",
stat="density",
)
axs[0, 1].set_title("Distribution of target for target=" + str(target_uniq[1]))
sns.histplot(
data=data[data[target] == target_uniq[1]],
x=predictor,
kde=True,
ax=axs[0, 1],
color="orange",
stat="density",
)
axs[1, 0].set_title("Boxplot w.r.t target")
sns.boxplot(data=data, x=target, y=predictor, ax=axs[1, 0], palette="gist_rainbow")
axs[1, 1].set_title("Boxplot (without outliers) w.r.t target")
sns.boxplot(
data=data,
x=target,
y=predictor,
ax=axs[1, 1],
showfliers=False,
palette="gist_rainbow",
)
plt.tight_layout()
plt.show()
Summary of EDA
Data Description:
- Dependent variable is the salary which is of categorical data type.
- age, capital gain, and capital loss are of integer type while other variables are of categorical type
- There are no missing values in the dataset.
Data Cleaning:
- We observed that all the observations where workclass = ? the values in the occupation are ?
- The strong pattern between workclass and occupation makes sense as both of these variables capture similar information.
- There is no strong correlation of ? observations in occupation and workclass with native_country.
- For now we will replaced these ?’s with the ‘unknown’ category.
- There are 42 distinct countries in the data set, which were reduced to their respective continents to reduce the dimension of data and we now have only 5 distinct values in the data.
- We reduced the distinct groups of marital_status to three categories: Married, Not-Married and Never-Married.
Observations from EDA:
In [ ]:
# creating histograms df_clean[numeric_cols].hist(figsize=(14, 14)) plt.show()
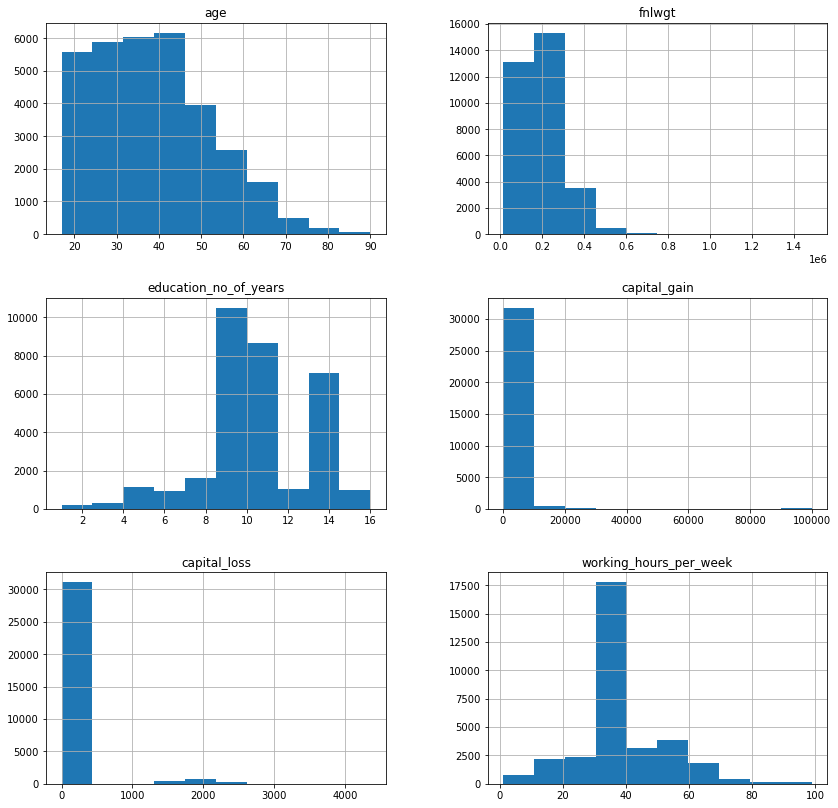
age: Average age of people in the dataset is 38 years, age has a wide range from 17 to 90 years.Age has a wide range of distribution in the interval of age ~ 18-90 years. From the distribution of this variable, we can observe that most of the people are aged around 25 – 40 years. We can infer from this data that the NGO is helping the adults to make the life of underprivileged people so that they can contribute in the overall development of the nation.education_no_of_years: The average education in years is 10 years. There’s a large difference between the minimum value and 25th percentile which indicates that there might be outliers present in this variable.capital_gain: There’s a huge difference in the 75th percentile and maximum value of capital_gain indicating the presence of outliers. Also, 75% of the observations are 0.capital_loss: Same as capital gain there’s a huge difference in the 75th percentile and maximum value indicating the presence of outliers. Also, 75% of the observations are 0.working_hours_per_week: On average people work for 40 hours a week. A vast difference in minimum value and 25th percentile, as well as 75th percentile and the maximum value, indicates that there might be outliers present in the variable.fnlwght: fnlwght is right-skewed. It has lots of outliers on the right side which we can cap.working_hours_per_week: Most of the data is concentrated around 40 working hours this gives a sense that most of the observations in data might be salaried employees working 8hrs 5 days a week. Some of the observations are clear outliers like working 1 hour a week which needs to be treated.workclass: ~70% of the observations are from the Private sector working class.marita_status: 47.3% of the observations in the dataset are married followed by 32.8% of the people who never married.race: * 94% of the people are native to north_america followed by 2.1% Asians.- Private sector employees work for more hours to get a salary above 50K.
- There’s large variability in the working hours of self-employed people which makes sense as they might be working at their ease.
Bivariate Analysis:
salary vs sex: ~25% of the males have salary >50K whereas only ~15% of the females have salary >50K.salary vs age:
In [ ]:
distribution_plot_wrt_target(df_clean, "age", "salary")
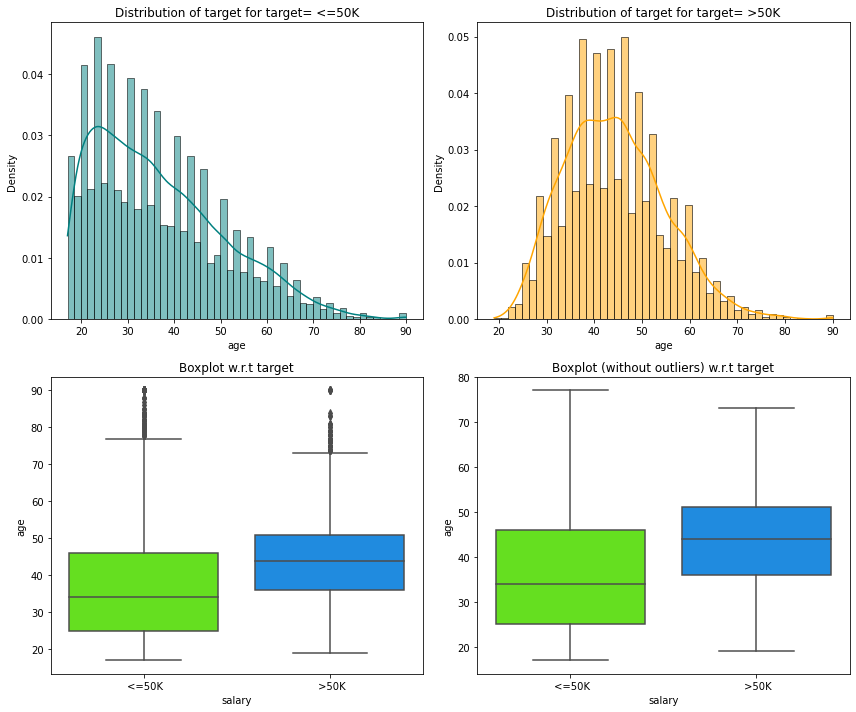
- People who more than 50K salary are generally older having an average age of around 48 years.
- People who have less than 50K salary have an average age of around 36.
salary vs occupation: –
In [ ]:
stacked_barplot(df_clean, "occupation", "salary")
salary <=50K >50K All occupation All 24720 7841 32561 Exec-managerial 2098 1968 4066 Prof-specialty 2281 1859 4140 Sales 2667 983 3650 Craft-repair 3170 929 4099 Adm-clerical 3263 507 3770 Transport-moving 1277 320 1597 Tech-support 645 283 928 Machine-op-inspct 1752 250 2002 Protective-serv 438 211 649 Unknown 1652 191 1843 Other-service 3158 137 3295 Farming-fishing 879 115 994 Handlers-cleaners 1284 86 1370 Armed-Forces 8 1 9 Priv-house-serv 148 1 149 ------------------------------------------------------------------------------------------------------------------------

- ~50% of the people whose occupation is of Executive Manager, Professor-speciality have a salary above 50,000 dollars. People with occupations like Private house service,handlers-cleaners, farming-fishing have a higher likelihood of having below 50K salary.
salary vs education:
In [ ]:
stacked_barplot(df_clean, "education", "salary")
salary <=50K >50K All education All 24720 7841 32561 Bachelors 3134 2221 5355 HS-grad 8826 1675 10501 Some-college 5904 1387 7291 Masters 764 959 1723 Prof-school 153 423 576 Assoc-voc 1021 361 1382 Doctorate 107 306 413 Assoc-acdm 802 265 1067 10th 871 62 933 11th 1115 60 1175 7th-8th 606 40 646 12th 400 33 433 9th 487 27 514 5th-6th 317 16 333 1st-4th 162 6 168 Preschool 51 0 51 ------------------------------------------------------------------------------------------------------------------------
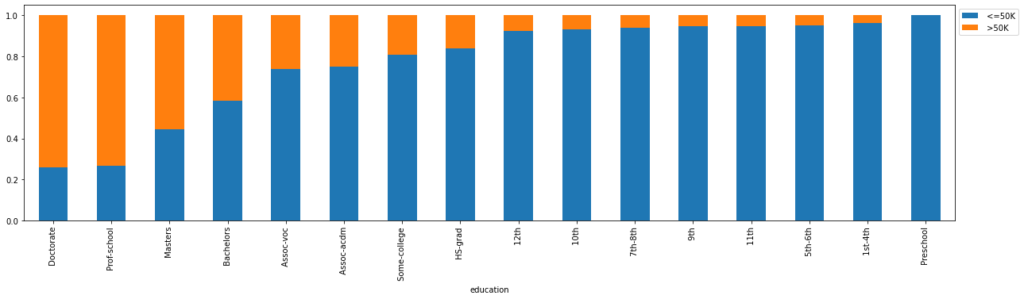
- ~70% of the people of are Doctorate, graduate from Professional school program (Prof-school) have a salary above 50K dollars
salary vs workclass:
In [ ]:
stacked_barplot(df_clean, "workclass", "salary")
salary <=50K >50K All workclass All 24720 7841 32561 Private 17733 4963 22696 Self-emp-not-inc 1817 724 2541 Self-emp-inc 494 622 1116 Local-gov 1476 617 2093 Federal-gov 589 371 960 State-gov 945 353 1298 Unknown 1645 191 1836 Never-worked 7 0 7 Without-pay 14 0 14 ------------------------------------------------------------------------------------------------------------------------
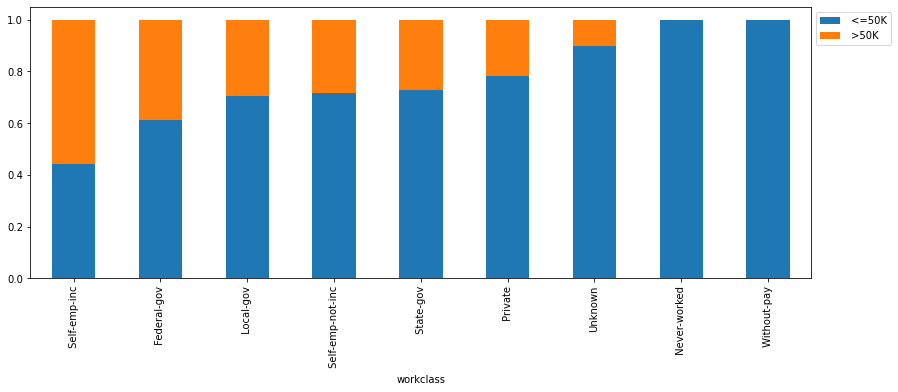
- ~50% of the self-employed people have a salary above 50K followed by ~40% of the federal govt employee who has salary more than 50K. ~20% of the people working in the private sector earn more than 50K.
salary vs working_hours_per_week:
In [ ]:
distribution_plot_wrt_target(df_clean, "working_hours_per_week", "salary")
- Majority of people having above 50K salary work around 40 hours per week.
salary vs native_country: More than 90% of the people from south_america are likely to have <=50k Salary. From asia and europe, around 70% of the people have <=50k salary.
Actions for data pre-processing:
- Many variables have outliers that need to be treated.
- We can drop capital_gain and capital_loss as most of the observations are 0 in these variables, and if the government already knows a person’s capital gain or loss it will be easier for them to classify a person into a salary group.
Data Pre-Processing
- Dropping capital_gain and capital_loss
- There are many outliers in the data which we will treat (perform capping of outliers).
- All the values smaller than the lower whisker will be assigned the value of the lower whisker, and all the values above the upper whisker will be assigned the value of the upper whisker.
Dropping capital_gain and capital_loss
In [ ]:
data.drop(["capital_gain", "capital_loss"], axis=1, inplace=True)
Outliers detection using boxplot
In [ ]:
numerical_col = data.select_dtypes(include=np.number).columns.tolist()
plt.figure(figsize=(20, 30))
for i, variable in enumerate(numerical_col):
plt.subplot(5, 4, i + 1)
plt.boxplot(data[variable], whis=1.5)
plt.tight_layout()
plt.title(variable)
plt.show()
- Age and fnlwgt have upper outliers.
- education_no_years has lower outliers.
- working_hours_per_week has both upper and lower outliers.
Treating Outliers
In [ ]:
# functions to treat outliers by flooring and capping
def treat_outliers(df, col):
"""
Treats outliers in a variable
df: dataframe
col: dataframe column
"""
Q1 = df[col].quantile(0.25) # 25th quantile
Q3 = df[col].quantile(0.75) # 75th quantile
IQR = Q3 - Q1
Lower_Whisker = Q1 - 1.5 * IQR
Upper_Whisker = Q3 + 1.5 * IQR
# all the values smaller than Lower_Whisker will be assigned the value of Lower_Whisker
# all the values greater than Upper_Whisker will be assigned the value of Upper_Whisker
df[col] = np.clip(df[col], Lower_Whisker, Upper_Whisker)
return df
def treat_outliers_all(df, col_list):
"""
Treat outliers in a list of variables
df: dataframe
col_list: list of dataframe columns
"""
for c in col_list:
df = treat_outliers(df, c)
return df
In [ ]:
numerical_col = data.select_dtypes(include=np.number).columns.tolist()
data = treat_outliers_all(data, numerical_col)
# let's look at box plot to see if outliers have been treated or not
plt.figure(figsize=(20, 30))
for i, variable in enumerate(numerical_col):
plt.subplot(5, 4, i + 1)
plt.boxplot(data[variable], whis=1.5)
plt.tight_layout()
plt.title(variable)
plt.show()
Data Preparation
Encoding >50K as 0 and <=50K as 1 as government wants to find underprivileged section of society.
In [ ]:
data["salary"] = data["salary"].apply(lambda x: 1 if x == " <=50K" else 0)
Creating training and test sets.
In [ ]:
X = data.drop(["salary"], axis=1)
Y = data["salary"]
X = pd.get_dummies(X, drop_first=True)
# Splitting data in train and test sets
X_train, X_test, y_train, y_test = train_test_split(
X, Y, test_size=0.30, random_state=1
)
In [ ]:
print("Shape of Training set : ", X_train.shape)
print("Shape of test set : ", X_test.shape)
print("Percentage of classes in training set:")
print(y_train.value_counts(normalize=True))
print("Percentage of classes in test set:")
print(y_test.value_counts(normalize=True))
Shape of Training set : (22792, 57) Shape of test set : (9769, 57) Percentage of classes in training set: 1 0.753335 0 0.246665 Name: salary, dtype: float64 Percentage of classes in test set: 1 0.772853 0 0.227147 Name: salary, dtype: float64
Building the model
Model evaluation criterion
Model can make wrong predictions as:
- Predicting a person has a salary <=50K but in reality the salary of the person is >50K.
- Predicting a person doesn’t have a salary <=50K but in reality the salary of the person is <=50k.
Which case is more important?
- Both the cases are important as:
- If we predict a person has a salary <=50K but actually the salary is >50K then a wrong person will be getting the benefits of the scheme and government might lose resources.
- If we predict a person doesn’t have a salary <=50K but actually the salary is <=50K that person will not be able to avail the benefits of the scheme constituting to opportunity loss.
How to reduce this loss i.e need to reduce False Negatives?
f1_scoreshould be maximized, the greater the f1_score higher the chances of identifying both the classes correctly.
First, let’s create functions to calculate different metrics and confusion matrix so that we don’t have to use the same code repeatedly for each model.
- The model_performance_classification_sklearn_with_threshold function will be used to check the model performance of models.
- The confusion_matrix_sklearn_with_threshold function will be used to plot confusion matrix.
In [ ]:
# defining a function to compute different metrics to check performance of a classification model built using sklearn
def model_performance_classification_sklearn_with_threshold(model, predictors, target, threshold=0.5):
"""
Function to compute different metrics, based on the threshold specified, to check classification model performance
model: classifier
predictors: independent variables
target: dependent variable
threshold: threshold for classifying the observation as class 1
"""
# predicting using the independent variables
pred_prob = model.predict_proba(predictors)[:, 1]
pred_thres = pred_prob > threshold
pred = np.round(pred_thres)
acc = accuracy_score(target, pred) # to compute Accuracy
recall = recall_score(target, pred) # to compute Recall
precision = precision_score(target, pred) # to compute Precision
f1 = f1_score(target, pred) # to compute F1-score
# creating a dataframe of metrics
df_perf = pd.DataFrame(
{
"Accuracy": acc,
"Recall": recall,
"Precision": precision,
"F1": f1,
},
index=[0],
)
return df_perf
In [ ]:
# defining a function to plot the confusion_matrix of a classification model built using sklearn
def confusion_matrix_sklearn_with_threshold(model, predictors, target, threshold=0.5):
"""
To plot the confusion_matrix, based on the threshold specified, with percentages
model: classifier
predictors: independent variables
target: dependent variable
threshold: threshold for classifying the observation as class 1
"""
pred_prob = model.predict_proba(predictors)[:, 1]
pred_thres = pred_prob > threshold
y_pred = np.round(pred_thres)
cm = confusion_matrix(target, y_pred)
labels = np.asarray(
[
["{0:0.0f}".format(item) + "\n{0:.2%}".format(item / cm.flatten().sum())]
for item in cm.flatten()
]
).reshape(2, 2)
plt.figure(figsize=(6, 4))
sns.heatmap(cm, annot=labels, fmt="")
plt.ylabel("True label")
plt.xlabel("Predicted label")
Logistic Regression
In [ ]:
# There are different solvers available in Sklearn logistic regression # The newton-cg solver is faster for high-dimensional data lg = LogisticRegression(solver="newton-cg", random_state=1) model = lg.fit(X_train, y_train)
Checking model performance on training set
In [ ]:
# creating confusion matrix confusion_matrix_sklearn_with_threshold(lg, X_train, y_train)

In [ ]:
log_reg_model_train_perf = model_performance_classification_sklearn_with_threshold(
lg, X_train, y_train
)
print("Training performance:")
log_reg_model_train_perf
Training performance:
Out[ ]:
| Accuracy | Recall | Precision | F1 | |
|---|---|---|---|---|
| 0 | 0.834328 | 0.921083 | 0.867241 | 0.893351 |
Checking performance on test set
In [ ]:
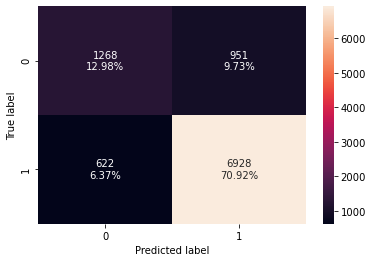
# creating confusion matrix confusion_matrix_sklearn_with_threshold(lg, X_test, y_test)
In [ ]:
log_reg_model_test_perf = model_performance_classification_sklearn_with_threshold(
lg, X_test, y_test
)
print("Test set performance:")
log_reg_model_test_perf
Test set performance:
Out[ ]:
| Accuracy | Recall | Precision | F1 | |
|---|---|---|---|---|
| 0 | 0.83898 | 0.917616 | 0.879299 | 0.898049 |
ROC-AUC
- The area under the ROC curve (AUC) is a measure of how good a model is – The higher the AUC, the better the model is, at distinguishing between classes.
1. predict_proba
Predicts the probabilities for the class 0 and 1.
Input: Train or test data
Output: Returns the predicted probabilities for class 0 and 1
2. roc_curve_score
Returns the auc scores
Input:
1. Training data
2. Predicted Probability
Output: AUC scores between 0 and 1
3. roc_curve
Returns the fpr, tpr and threshold values which takes the original data and predicted probabilities for the class 1.
Input:
1. Training data
2. Predicted Probability
Output: False positive rate, true positive rate and threshold values
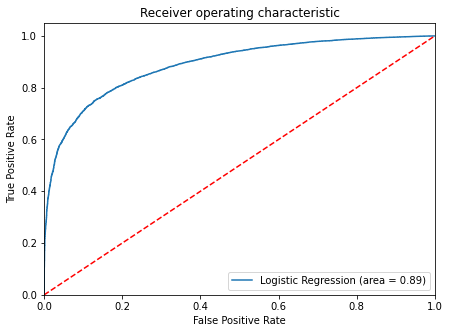
- ROC-AUC on training set
In [ ]:
# Find the roc auc score for training data
logit_roc_auc_train = roc_auc_score(
y_train, lg.predict_proba(X_train)[:, 1]
) # The indexing represents predicted probabilities for class 1
# Find fpr, tpr and threshold values
fpr, tpr, thresholds = roc_curve(y_train, lg.predict_proba(X_train)[:, 1])
plt.figure(figsize=(7, 5))
# Plot roc curve
plt.plot(fpr, tpr, label="Logistic Regression (area = %0.2f)" % logit_roc_auc_train)
plt.plot([0, 1], [0, 1], "r--")
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiver operating characteristic")
plt.legend(loc="lower right")
plt.show()
- ROC-AUC on test set
In [ ]:
# Find the roc auc score for training data
logit_roc_auc_test = roc_auc_score(
y_test, lg.predict_proba(X_test)[:, 1]
) # The indexing represents predicted probabilities for class 1
# Find fpr, tpr and threshold values
fpr, tpr, thresholds = roc_curve(y_test, lg.predict_proba(X_test)[:, 1])
plt.figure(figsize=(7, 5))
# Plot roc curve
plt.plot(fpr, tpr, label="Logistic Regression (area = %0.2f)" % logit_roc_auc_test)
plt.plot([0, 1], [0, 1], "r--")
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiver operating characteristic")
plt.legend(loc="lower right")
plt.show()
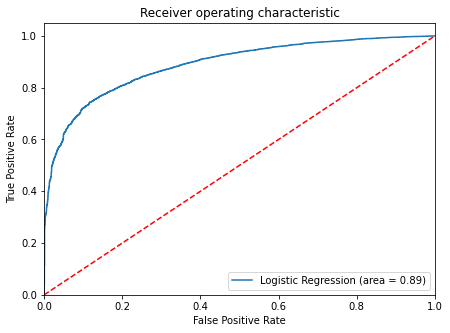
- Model is giving a generalized performance.
Model Performance Improvement
- Let’s see if the f1 score can be improved further, by changing the model threshold using AUC-ROC Curve.
Optimal threshold using AUC-ROC curve
Optimal thresold is the value that best separated the True positive rate and False positive rate.
In [ ]:
# Optimal threshold as per AUC-ROC curve
# The optimal cut off would be where tpr is high and fpr is low
# roc_curve returns the fpr, tpr and threshold values which takes the original data and predicted probabilities for the class 1.
fpr, tpr, thresholds = roc_curve(
y_train, lg.predict_proba(X_train)[:, 1]
) # The indexing represents predicted probabilities for class 1
optimal_idx = np.argmax(
tpr - fpr
) # Finds the index that contains the max difference between tpr and fpr
optimal_threshold_auc_roc = thresholds[
optimal_idx
] # stores the optimal threshold value
print(optimal_threshold_auc_roc)
0.7757843488056327
Checking model performance on training set
In [ ]:
# creating confusion matrix
confusion_matrix_sklearn_with_threshold(
lg, X_train, y_train, threshold=optimal_threshold_auc_roc
)
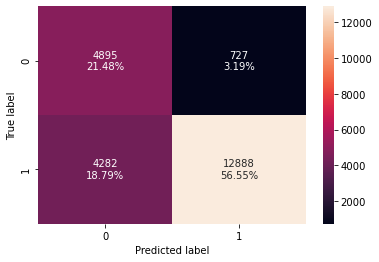
In [ ]:
# checking model performance for this model
log_reg_model_train_perf_threshold_auc_roc = model_performance_classification_sklearn_with_threshold(
lg, X_train, y_train, threshold=optimal_threshold_auc_roc
)
print("Training performance:")
log_reg_model_train_perf_threshold_auc_roc
Training performance:
Out[ ]:
| Accuracy | Recall | Precision | F1 | |
|---|---|---|---|---|
| 0 | 0.78023 | 0.750612 | 0.946603 | 0.837291 |
Checking model performance on test set
In [ ]:
# creating confusion matrix
confusion_matrix_sklearn_with_threshold(
lg, X_test, y_test, threshold=optimal_threshold_auc_roc
)
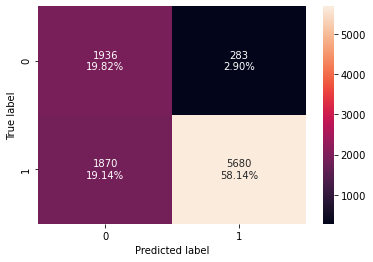
In [ ]:
# checking model performance for this model
log_reg_model_test_perf_threshold_auc_roc = model_performance_classification_sklearn_with_threshold(
lg, X_test, y_test, threshold=optimal_threshold_auc_roc
)
print("Test set performance:")
log_reg_model_test_perf_threshold_auc_roc
Test set performance:
Out[ ]:
| Accuracy | Recall | Precision | F1 | |
|---|---|---|---|---|
| 0 | 0.779609 | 0.752318 | 0.952541 | 0.840672 |
- The precision of the model for both training and test set has improved but the F1 score has reduced.
Let’s use Precision-Recall curve and see if we can find a better threshold
The Precision-Recall curve shows the tradeoff between Precision and Recall for different thresholds. It can be used to select optimal threshold as required to improve the model improvement.
precision_recall_curve()
Returns the fpr, tpr and threshold values
Input:
1. Original data
2. Predicted Probability
Output: False positive rate, true positive rate and threshold values
In [ ]:
# Find the predicted probabilities for class 1
y_scores = lg.predict_proba(X_train)[:, 1]
# Find fpr, tpr and threshold values
prec, rec, tre = precision_recall_curve(y_train, y_scores,)
def plot_prec_recall_vs_tresh(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="precision")
plt.plot(thresholds, recalls[:-1], "g--", label="recall")
plt.xlabel("Threshold")
plt.legend(loc="upper left")
plt.ylim([0, 1])
plt.figure(figsize=(10, 7))
# Plot recall precision curve
plot_prec_recall_vs_tresh(prec, rec, tre)
plt.show()
- At the threshold of 0.58, we get balanced recall and precision.
In [ ]:
# setting the threshold optimal_threshold_curve = 0.58
Checking model performance on training set
In [ ]:
# creating confusion matrix
confusion_matrix_sklearn_with_threshold(
lg, X_train, y_train, threshold=optimal_threshold_curve
)
In [ ]:
log_reg_model_train_perf_threshold_curve = model_performance_classification_sklearn_with_threshold(
lg, X_train, y_train, threshold=optimal_threshold_curve
)
print("Training performance:")
log_reg_model_train_perf_threshold_curve
Training performance:
Out[ ]:
| Accuracy | Recall | Precision | F1 | |
|---|---|---|---|---|
| 0 | 0.831739 | 0.886954 | 0.889389 | 0.88817 |
Checking model performance on test set
In [ ]:
# creating confusion matrix
confusion_matrix_sklearn_with_threshold(
lg, X_test, y_test, threshold=optimal_threshold_curve
)
In [ ]:
log_reg_model_test_perf_threshold_curve = model_performance_classification_sklearn_with_threshold(
lg, X_test, y_test, threshold=optimal_threshold_curve
)
print("Test set performance:")
log_reg_model_test_perf_threshold_curve
Test set performance:
Out[ ]:
| Accuracy | Recall | Precision | F1 | |
|---|---|---|---|---|
| 0 | 0.831508 | 0.880927 | 0.899027 | 0.889885 |
- Model is performing well on training and test.
- There’s not much improvement in the model performance as the default threshold is 0.50 and here we get 0.58 as the optimal threshold.
Model Performance Summary
In [ ]:
# training performance comparison
models_train_comp_df = pd.concat(
[
log_reg_model_train_perf.T,
log_reg_model_train_perf_threshold_auc_roc.T,
log_reg_model_train_perf_threshold_curve.T,
],
axis=1,
)
models_train_comp_df.columns = [
"Logistic Regression sklearn",
"Logistic Regression-0.77 Threshold",
"Logistic Regression-0.58 Threshold",
]
print("Training performance comparison:")
models_train_comp_df
Training performance comparison:
Out[ ]:
| Logistic Regression sklearn | Logistic Regression-0.77 Threshold | Logistic Regression-0.58 Threshold | |
|---|---|---|---|
| Accuracy | 0.834328 | 0.780230 | 0.831739 |
| Recall | 0.921083 | 0.750612 | 0.886954 |
| Precision | 0.867241 | 0.946603 | 0.889389 |
| F1 | 0.893351 | 0.837291 | 0.888170 |
In [ ]:
# testing performance comparison
models_test_comp_df = pd.concat(
[
log_reg_model_test_perf.T,
log_reg_model_test_perf_threshold_auc_roc.T,
log_reg_model_test_perf_threshold_curve.T,
],
axis=1,
)
models_test_comp_df.columns = [
"Logistic Regression sklearn",
"Logistic Regression-0.77 Threshold",
"Logistic Regression-0.58 Threshold",
]
print("Test set performance comparison:")
models_test_comp_df
Test set performance comparison:
Out[ ]:
| Logistic Regression sklearn | Logistic Regression-0.77 Threshold | Logistic Regression-0.58 Threshold | |
|---|---|---|---|
| Accuracy | 0.838980 | 0.779609 | 0.831508 |
| Recall | 0.917616 | 0.752318 | 0.880927 |
| Precision | 0.879299 | 0.952541 | 0.899027 |
| F1 | 0.898049 | 0.840672 | 0.889885 |
Conclusion
- We have been able to build a predictive model that can be used by the government to find the citizens having less than 50K salary with an f1_score of 0.89 on the training set and formulate policies accordingly.
- From the analysis, factors like age, working hours per week will lead to decrease in chances of a person having <=50K salary and workclass, occupations like private house servive, other services will lead to increase in chances of a person having <=50K salary.
Recommendations
- The government should promote education among citizens, they should make policies to make education accessible to all, as we saw in our analysis that people who have higher education are more likely to have a salary above 50,000 Dollars.
- Working hours is one of the significant predictors of salary, The government should implement laws to ensure that people are paid fairly for their work and are not overworked for the increase in salaries. This would improve work-life balance.
- People who invest more are more likely to have a salary above 50k, government should initiate investment schemes and facilitate ease of investment so that people can plan and invest in resources.
- As we saw in our analysis that Asian-Pac-Islander and White people are paid more than other races, there should be reforms to ensure that the salary criterion of employees is independent of their race.
- Reforms should be made for private-sector employees so that they are paid fairly for their work.
- Policy formulated by the government should be considerate of equal pay and counter the pay gap that exists in society.
Appendix
Univariate Analysis on Numerical data
In [ ]:
# creating histograms df_clean[numeric_cols].hist(figsize=(14, 14)) plt.show()
Observations
- Age has a wide range of distribution in the interval of age ~ 18-90 years. From the distribution of this variable, we can observe that most of the people are aged around 25 – 40 years. We can infer from this data that the NGO is helping the adults to make the life of underprivileged people so that they can contribute in the overall development of the nation.
- fnlwgt has a skewed distribution. It indicates that the weights assigned by CPS lie in the range 0.1-0.7.
- The distribution of the education_no_of_year indicates that most of the people have at least 8-11 years of education.
- capital_gain indicates that for most people investment gain and less than 10000.
- capital_loss distribution shows that most people do not have a loss of more than 300. There are few people who have investment loss of around 2000.
- The distribution of working_hours_per_week indicates that the people work for around 40-50 hours every week and there are some exceptions who work even more than 50 hours.
Univariate Analysis on Categorical data
In [ ]:
## Barplot for the categorical features
for i in cat_cols:
print(i)
labeled_barplot(df_clean, i, perc=True)
plt.show()
print(
" ****************************************************************** "
) ## To create a separator
workclass
****************************************************************** education
****************************************************************** marital_status
****************************************************************** occupation
****************************************************************** relationship
****************************************************************** race
****************************************************************** sex
****************************************************************** native_country
****************************************************************** salary
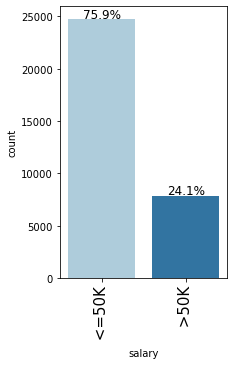
******************************************************************
Observations
- According to the workclass feature, ~70% of the observations are from the Private sector working class. As expected from the number of hours per week.
- From the education column it can be inferred that more than 50% of the observations are at least HS grads or have gone to some college.
- In the marital_status feature, 46.1% of the observations in the dataset are married followed by 32.8% of the people who never married.
- The Occupation of people is some clerical work, sales, or service-based.
- The relationship
- The race of 85% of the observations is white.
- The sex of the 67% of the population is male and the remaining are female.
- 94% of the people are native_country to north_america followed by 2.1% Asians.
- 24% of the observations have a salary above 50K and while 76% have a salary below 50K
Bivariate Analysis
Correlation Plot
In [ ]:
plt.figure(figsize=(15, 7)) sns.heatmap(df_clean.corr(), annot=True, vmin=-1, vmax=1, fmt=".2f", cmap="Spectral") plt.show()
- There is no significant correlation between the columns.
Exploring the categorical data with respect to the target
In [ ]:
stacked_barplot(df_clean, "native_country", "salary")
salary <=50K >50K All native_country All 24720 7841 32561 north_america 23275 7313 30588 asia 465 206 671 other 501 162 663 europe 369 152 521 south_america 110 8 118 ------------------------------------------------------------------------------------------------------------------------
- More than 90% of the people from south_america are likely to have <=50k Salary. From asia and europe, around 70% of the people have <=50k salary.
Sex vs Salary
In [ ]:
stacked_barplot(df_clean, "sex", "salary")
salary <=50K >50K All sex All 24720 7841 32561 Male 15128 6662 21790 Female 9592 1179 10771 ------------------------------------------------------------------------------------------------------------------------
- ~25% of the males have salary >50K whereas only ~15% of the females have salary >50K.
- This shows the pay gap that exists in society and the government should investigate further on it to formulate policy to ensure equal pay.
Salary vs education
In [ ]:
stacked_barplot(df_clean, "education", "salary")
salary <=50K >50K All education All 24720 7841 32561 Bachelors 3134 2221 5355 HS-grad 8826 1675 10501 Some-college 5904 1387 7291 Masters 764 959 1723 Prof-school 153 423 576 Assoc-voc 1021 361 1382 Doctorate 107 306 413 Assoc-acdm 802 265 1067 10th 871 62 933 11th 1115 60 1175 7th-8th 606 40 646 12th 400 33 433 9th 487 27 514 5th-6th 317 16 333 1st-4th 162 6 168 Preschool 51 0 51 ------------------------------------------------------------------------------------------------------------------------
- ~70% of the people of are Doctorate, graduate from Professional school program (Prof-school) have a salary above $50K.
- This clearly shows a positive relationship between education and salary, the higher the education higher is the salary.
Salary vs occupation
In [ ]:
stacked_barplot(df_clean, "occupation", "salary")
salary <=50K >50K All occupation All 24720 7841 32561 Exec-managerial 2098 1968 4066 Prof-specialty 2281 1859 4140 Sales 2667 983 3650 Craft-repair 3170 929 4099 Adm-clerical 3263 507 3770 Transport-moving 1277 320 1597 Tech-support 645 283 928 Machine-op-inspct 1752 250 2002 Protective-serv 438 211 649 Unknown 1652 191 1843 Other-service 3158 137 3295 Farming-fishing 879 115 994 Handlers-cleaners 1284 86 1370 Armed-Forces 8 1 9 Priv-house-serv 148 1 149 ------------------------------------------------------------------------------------------------------------------------
- ~50% of the people whose occupation is of Executive Manager, Professor-speciality have a salary above $50,000
- People with occupations like Private house service,handlers-cleaners, farming-fishing have a higher likelihood of having below 50K salary.
Salary vs race
In [ ]:
stacked_barplot(df_clean, "race", "salary")
salary <=50K >50K All race All 24720 7841 32561 White 20699 7117 27816 Black 2737 387 3124 Asian-Pac-Islander 763 276 1039 Amer-Indian-Eskimo 275 36 311 Other 246 25 271 ------------------------------------------------------------------------------------------------------------------------
- 25% of the White and Asia-Pacific people have a salary more than 50K salary as compared to people from other race.
Salary vs workclass
In [ ]:
stacked_barplot(df_clean, "workclass", "salary")
salary <=50K >50K All workclass All 24720 7841 32561 Private 17733 4963 22696 Self-emp-not-inc 1817 724 2541 Self-emp-inc 494 622 1116 Local-gov 1476 617 2093 Federal-gov 589 371 960 State-gov 945 353 1298 Unknown 1645 191 1836 Never-worked 7 0 7 Without-pay 14 0 14 ------------------------------------------------------------------------------------------------------------------------
- ~50% of the self-employed people have a salary above 50K followed by ~40% of the federal govt employee who has salary more than 50K.
- ~20% of the people working in the private sector earn more than 50K.
Salary vs marital_status
In [ ]:
stacked_barplot(df_clean, "marital_status", "salary")
salary <=50K >50K All marital_status All 24720 7841 32561 married 8297 6702 14999 not_married 6231 648 6879 Never-married 10192 491 10683 ------------------------------------------------------------------------------------------------------------------------
- Married people have a higher likelihood of getting a salary above 50K compared to Never Married and Not married people.
Exploring the categorical data with respect to the target
Salary vs age
In [ ]:
distribution_plot_wrt_target(df_clean, "age", "salary")
- People who more than 50K salary are generally older having an average age of around 48 years.
- People who have less than 50K salary have an average age of around 36.
Salary vs working_hours_per_week
In [ ]:
distribution_plot_wrt_target(df_clean, "working_hours_per_week", "salary")
- Majority of people having above 50K salary work around 40 hours per week.
- Those having >50K salary have a higher range of working hours as compared to the ones with <=50K, but there are outliers present.
In [ ]:
# lets see how working hours per week vary across different occupation
plt.figure(figsize=(15, 12))
sns.boxplot(
y="workclass",
x="working_hours_per_week",
data=df_clean,
hue="salary",
showfliers=False,
)
plt.show()
- Private sector employees work for more hours to get a salary above 50K.
- There’s large variability in the working hours of self-employed people which makes sense as they might be working at their ease.
- Without pay and never worked will have no income or less than 50K income.
- The number of working hours for many government employees is concentrated at 40 hrs a week, which makes sense as government employees generally have fixed working hours.