Linear Regression Model in Data Science

To understand how to fit a given set of data into a Linear Regression Model, let’s go through an example.

We will construct a linear model that explains the relationship a car’s mileage (mpg) has with its other attributes

Import Libraries

In [1]:

import numpy as np   
from sklearn.linear_model import LinearRegression
import pandas as pd    
import matplotlib.pyplot as plt 
%matplotlib inline 
import seaborn as sns
from sklearn.model_selection import train_test_split # Sklearn package's randomized data splitting function

C:\Users\Rajet singh\Anaconda3\lib\site-packages\statsmodels\tools\_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
  import pandas.util.testing as tm

Load and review data

In [2]:

cData = pd.read_csv("auto-mpg.csv")  
cData.shape

Out[2]:

(398, 9)

In [3]:

# 8 variables: 
#
# MPG (miles per gallon), 
# cylinders, 
# engine displacement (cu. inches), 
# horsepower,
# vehicle weight (lbs.), 
# time to accelerate from O to 60 mph (sec.),
# model year (modulo 100), and 
# origin of car (1. American, 2. European,3. Japanese).
#
# Also provided are the car labels (types) 
# Missing data values are marked by series of question marks.


cData.head()

Out[3]:

	mpg	cylinders	displacement	horsepower	weight	acceleration	model year	origin	car name
0	18.0	8	307.0	130	3504	12.0	70	1	chevrolet chevelle malibu
1	15.0	8	350.0	165	3693	11.5	70	1	buick skylark 320
2	18.0	8	318.0	150	3436	11.0	70	1	plymouth satellite
3	16.0	8	304.0	150	3433	12.0	70	1	amc rebel sst
4	17.0	8	302.0	140	3449	10.5	70	1	ford torino

In [4]:

#dropping/ignoring car_name 
cData = cData.drop('car name', axis=1)
# Also replacing the categorical var with actual values
cData['origin'] = cData['origin'].replace({1: 'america', 2: 'europe', 3: 'asia'})
cData.head()

Out[4]:

	mpg	cylinders	displacement	horsepower	weight	acceleration	model year	origin
0	18.0	8	307.0	130	3504	12.0	70	america
1	15.0	8	350.0	165	3693	11.5	70	america
2	18.0	8	318.0	150	3436	11.0	70	america
3	16.0	8	304.0	150	3433	12.0	70	america
4	17.0	8	302.0	140	3449	10.5	70	america

Create Dummy Variables

Values like ‘america’ cannot be read into an equation. Using substitutes like 1 for america, 2 for europe and 3 for asia would end up implying that european cars fall exactly half way between american and asian cars! we dont want to impose such an baseless assumption!

So we create 3 simple true or false columns with titles equivalent to “Is this car America?”, “Is this care European?” and “Is this car Asian?”. These will be used as independent variables without imposing any kind of ordering between the three regions.

In [5]:

cData = pd.get_dummies(cData, columns=['origin'])
cData.head()

Out[5]:

	mpg	cylinders	displacement	horsepower	weight	acceleration	model year	origin_america	origin_asia	origin_europe
0	18.0	8	307.0	130	3504	12.0	70	1	0	0
1	15.0	8	350.0	165	3693	11.5	70	1	0	0
2	18.0	8	318.0	150	3436	11.0	70	1	0	0
3	16.0	8	304.0	150	3433	12.0	70	1	0	0
4	17.0	8	302.0	140	3449	10.5	70	1	0	0

Dealing with Missing Values

In [6]:

#A quick summary of the data columns
cData.describe()

Out[6]:

	mpg	cylinders	displacement	weight	acceleration	model year	origin_america	origin_asia	origin_europe
count	398.000000	398.000000	398.000000	398.000000	398.000000	398.000000	398.000000	398.000000	398.000000
mean	23.514573	5.454774	193.425879	2970.424623	15.568090	76.010050	0.625628	0.198492	0.175879
std	7.815984	1.701004	104.269838	846.841774	2.757689	3.697627	0.484569	0.399367	0.381197
min	9.000000	3.000000	68.000000	1613.000000	8.000000	70.000000	0.000000	0.000000	0.000000
25%	17.500000	4.000000	104.250000	2223.750000	13.825000	73.000000	0.000000	0.000000	0.000000
50%	23.000000	4.000000	148.500000	2803.500000	15.500000	76.000000	1.000000	0.000000	0.000000
75%	29.000000	8.000000	262.000000	3608.000000	17.175000	79.000000	1.000000	0.000000	0.000000
max	46.600000	8.000000	455.000000	5140.000000	24.800000	82.000000	1.000000	1.000000	1.000000

In [7]:

# hp is missing cause it does not seem to be reqcognized as a numerical column!
cData.dtypes

Out[7]:

mpg               float64
cylinders           int64
displacement      float64
horsepower         object
weight              int64
acceleration      float64
model year          int64
origin_america      uint8
origin_asia         uint8
origin_europe       uint8
dtype: object

In [8]:

# isdigit()? on 'horsepower' 
hpIsDigit = pd.DataFrame(cData.horsepower.str.isdigit())  # if the string is made of digits store True else False

#print isDigit = False!
cData[hpIsDigit['horsepower'] == False]   # from temp take only those rows where hp has false

Out[8]:

	mpg	cylinders	displacement	horsepower	weight	acceleration	model year	origin_america	origin_asia	origin_europe
32	25.0	4	98.0	?	2046	19.0	71	1	0	0
126	21.0	6	200.0	?	2875	17.0	74	1	0	0
330	40.9	4	85.0	?	1835	17.3	80	0	0	1
336	23.6	4	140.0	?	2905	14.3	80	1	0	0
354	34.5	4	100.0	?	2320	15.8	81	0	0	1
374	23.0	4	151.0	?	3035	20.5	82	1	0	0

In [9]:

# Missing values have a'?''
# Replace missing values with NaN
cData = cData.replace('?', np.nan)
cData[hpIsDigit['horsepower'] == False] 

Out[9]:

	mpg	cylinders	displacement	horsepower	weight	acceleration	model year	origin_america	origin_asia	origin_europe
32	25.0	4	98.0	NaN	2046	19.0	71	1	0	0
126	21.0	6	200.0	NaN	2875	17.0	74	1	0	0
330	40.9	4	85.0	NaN	1835	17.3	80	0	0	1
336	23.6	4	140.0	NaN	2905	14.3	80	1	0	0
354	34.5	4	100.0	NaN	2320	15.8	81	0	0	1
374	23.0	4	151.0	NaN	3035	20.5	82	1	0	0

There are various ways to handle missing values. Drop the rows, replace missing values with median values etc. of the 398 rows 6 have NAN in the hp column. We could drop those 6 rows – which might not be a good idea under all situations

In [10]:

#instead of dropping the rows, lets replace the missing values with median value. 
cData.median()

Out[10]:

mpg                 23.0
cylinders            4.0
displacement       148.5
horsepower          93.5
weight            2803.5
acceleration        15.5
model year          76.0
origin_america       1.0
origin_asia          0.0
origin_europe        0.0
dtype: float64

In [11]:

# replace the missing values with median value.
# Note, we do not need to specify the column names below
# every column's missing value is replaced with that column's median respectively  (axis =0 means columnwise)
#cData = cData.fillna(cData.median())

medianFiller = lambda x: x.fillna(x.median())
cData = cData.apply(medianFiller,axis=0)

cData['horsepower'] = cData['horsepower'].astype('float64')  # converting the hp column from object / string type to float

BiVariate Plots

A bivariate analysis among the different variables can be done using scatter matrix plot. Seaborn libs create a dashboard reflecting useful information about the dimensions. The result can be stored as a .png file.

In [12]:

cData_attr = cData.iloc[:, 0:7]
sns.pairplot(cData_attr, diag_kind='kde')   # to plot density curve instead of histogram on the diag

Out[12]:

<seaborn.axisgrid.PairGrid at 0x2aba2117108>

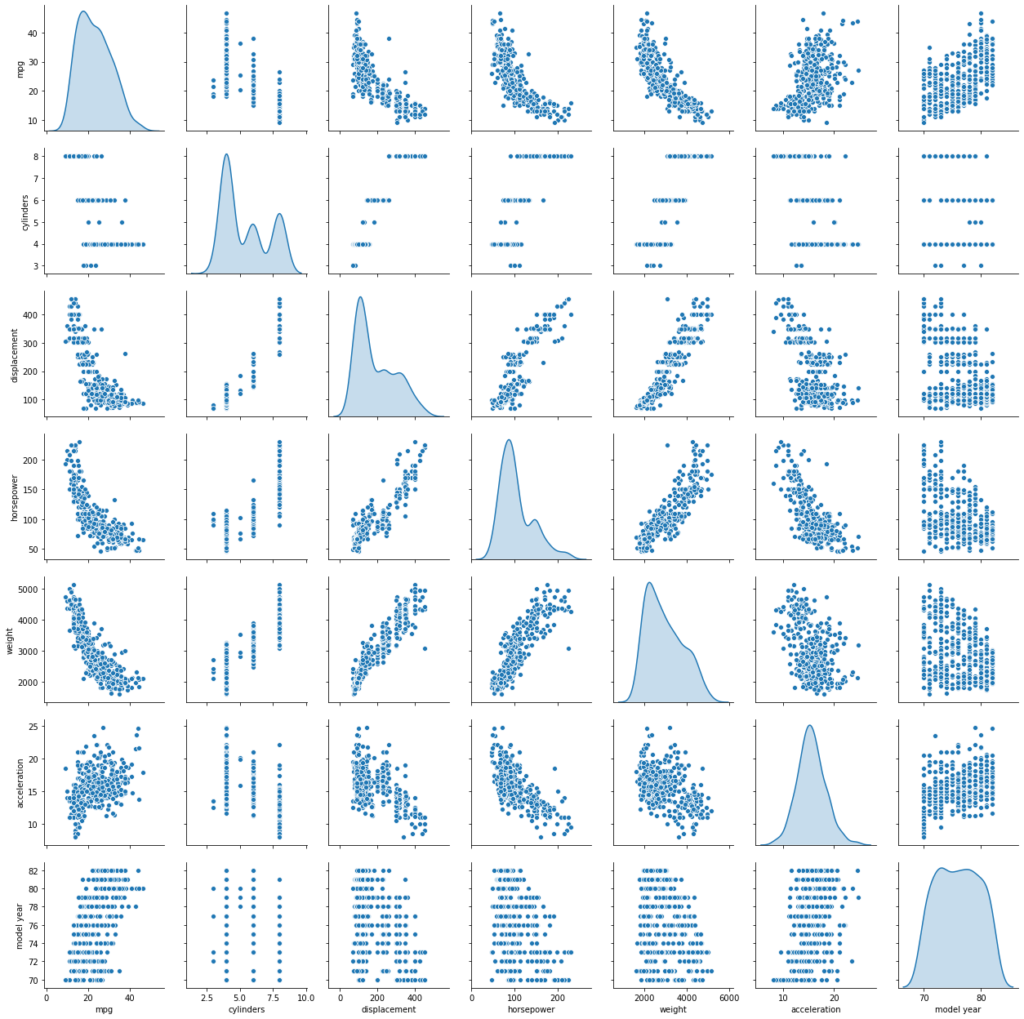
Observation between ‘mpg’ and other attributes indicate the relationship is not really linear. However, the plots also indicate that linearity would still capture quite a bit of useful information/pattern. Several assumptions of classical linear regression seem to be violated, including the assumption of no Heteroscedasticity

Split Data

In [13]:

# lets build our linear model
# independant variables
X = cData.drop(['mpg','origin_europe'], axis=1)
# the dependent variable
y = cData[['mpg']]

In [14]:

# Split X and y into training and test set in 70:30 ratio

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=1)

Fit Linear Model

In [15]:

regression_model = LinearRegression()
regression_model.fit(X_train, y_train)

Out[15]:

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

Here are the coefficients for each variable and the intercept

In [16]:

for idx, col_name in enumerate(X_train.columns):
    print("The coefficient for {} is {}".format(col_name, regression_model.coef_[0][idx]))

The coefficient for cylinders is -0.3948079661648244
The coefficient for displacement is 0.028945510765487174
The coefficient for horsepower is -0.02175220772354676
The coefficient for weight is -0.007352032065147351
The coefficient for acceleration is 0.061919366007618326
The coefficient for model year is 0.8369338917644993
The coefficient for origin_america is -3.0012830009185123
The coefficient for origin_asia is -0.6060179643247369

In [17]:

intercept = regression_model.intercept_[0]
print("The intercept for our model is {}".format(intercept))

The intercept for our model is -18.283451116372067

The score (R^2) for in-sample and out of sample

In [18]:

regression_model.score(X_train, y_train)

Out[18]:

0.8141025501610559

In [19]:

#out of sample score (R^2)

regression_model.score(X_test, y_test)

Out[19]:

0.8433135132808833

Adding interaction terms

In [20]:

from sklearn.preprocessing import PolynomialFeatures
from sklearn import linear_model

poly = PolynomialFeatures(degree=2, interaction_only=True)
X_train2 = poly.fit_transform(X_train)
X_test2 = poly.fit_transform(X_test)

poly_clf = linear_model.LinearRegression()

poly_clf.fit(X_train2, y_train)

y_pred = poly_clf.predict(X_test2)

#print(y_pred)

#In sample (training) R^2 will always improve with the number of variables!
print(poly_clf.score(X_train2, y_train))

0.9015975294607972

In [21]:

#Out off sample (testing) R^2 is our measure of sucess and does improve
print(poly_clf.score(X_test2, y_test))

0.8647441061208313

In [22]:

# but this improves as the cost of 29 extra variables!
print(X_train.shape)
print(X_train2.shape)

(278, 8)
(278, 37)

Polynomial Features (with only interaction terms) have improved the Out of sample R^2. However at the cost of increaing the number of variables significantly.